某简支梁有限元结构静力分析

刘浩,2010年8月4日

0   前言
     本文利用有限元计算软件ANSYS以及SAP2000对建立的钢筋混凝土简支梁模型进行了静力分析，并通过力学方法验证了其正确性。
1   概述
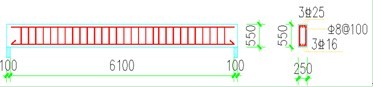
    如下图所示的钢筋混凝土梁，其横截面尺寸为b×h=250mm×550mm，梁的跨度为L=6.3m，下部刚性支座宽度为100mm，采用C25混凝土，梁内受拉纵筋316，架立筋采用325，箍筋采用8@ 100，钢筋保护层厚度为30mm。对于梁中采用的所有钢筋，弹性模量为2.0×105MPa，抗拉强度设计值360MPa，泊松比为0.3。根据混凝土设计规范，C25混凝土的弹性模量.8×104MPa，混凝土轴心抗压强度设计值为11.9 MPa，轴心抗拉强度设计值为1.27 MPa。该钢筋混凝土梁简支梁受竖向均布力120kN/m2，边界条件按照简支梁施加相应约束。

 

2   利用ANSYS软件建立模型与求解
     本文采用了3种不同的单元类型分别对该简支梁进行了建模：
2.1 采用BEAM4单元进行建模
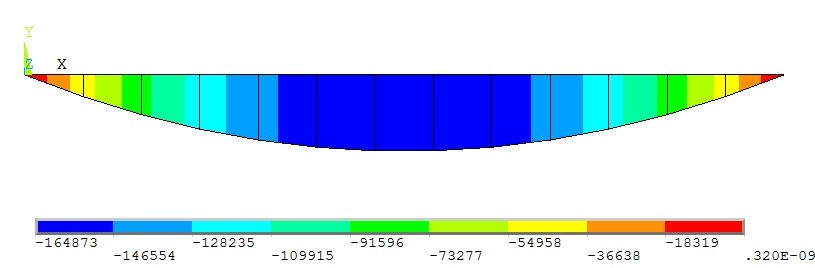
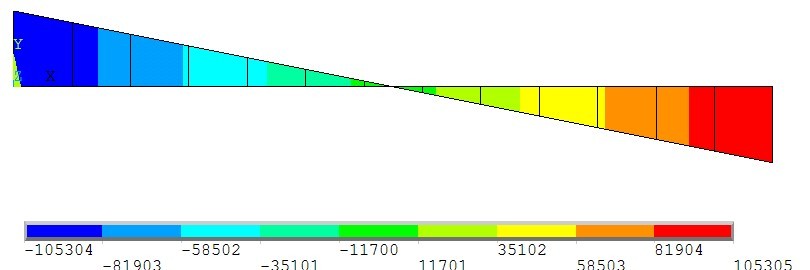
     BEAM4单元是一种可用于承受拉、压、弯、扭的三维弹性单元。这种单元在每个节点上有六个自由度。其基于结构力学经典梁弯曲理论构造的梁单元，忽略剪切变形的影响，应用了中线的法线在变形后仍保持和中面垂直的直法线假设。荷载施加运用两种情况：将重力折算为均布荷载施加在梁上表面；运用施加重力加速的方法施加重力。通过计算，知两种方法结果相同。结构的弯矩图和剪力图所示：

               

2.2 采用SOLID45单元进行建模
     此方法为实体建模方法，运用SOLID45单元对简支梁进行了建模，在参数设定过程中，均只设定了材料的弹性相关参数。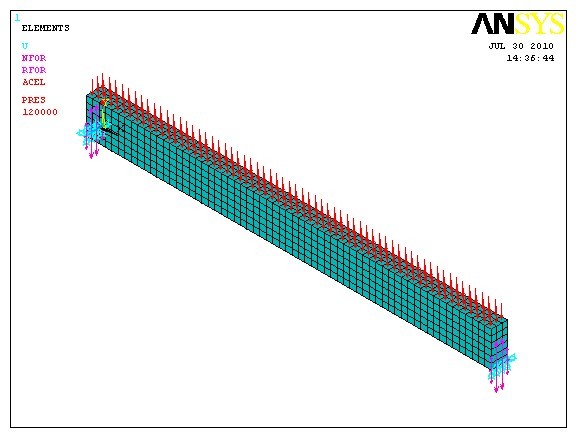

    简支梁跨中文件结果文件提取：
    FX  =  0.5127912E-04 kN
    FY  =  -1671.875 kN
    FZ  =   0.7224784E-07 kN
    MX  =  0.1688685E-07 kN.m
    MY  =  0.2893803E-06 kN.m
    MZ  =  165850.0 kN.m

2.3 采用 SOLID65+LINK8单元进行建模
    此方法为实体建模，模型中采用SOLID65单元模拟了混凝土，LINK8单元模拟了钢筋。这种建模方法除了可以提取跨中弯矩以及支座反力之外，还可以观察混凝土以及钢筋单元的应力分布等等，适用于局部节点分析。模型如下图所示：

 

 

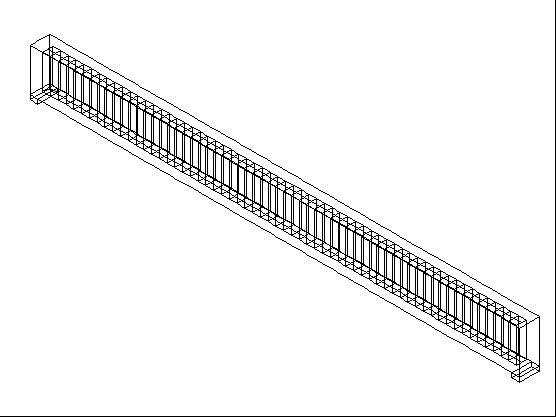
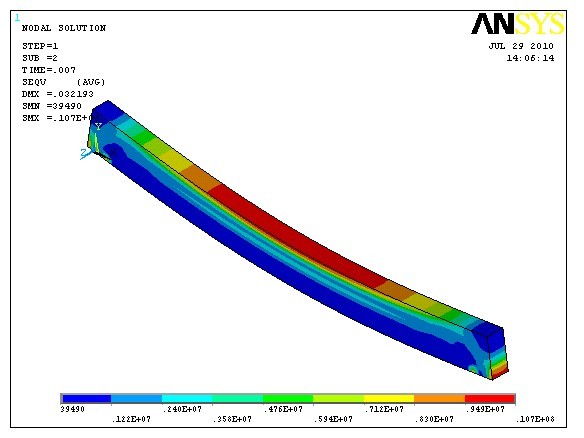
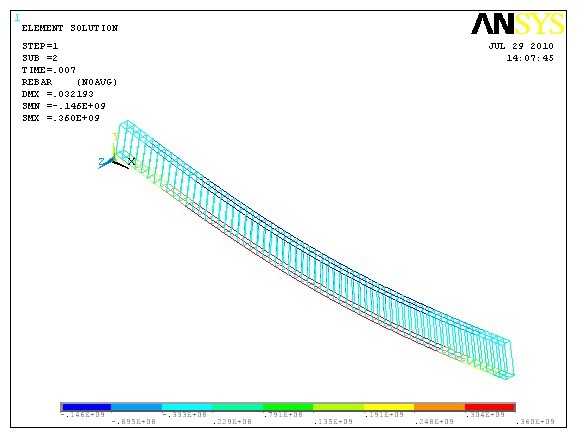
    简支梁跨中内力结果文件提取：
    FX  =  -0.6209011E-05 kN
    FY  =  -1671.875 kN
    FZ  =  -0.1403326E-03 kN
    MX  =  -417.9688 kN.m
    MY  =  0.1339622E-03 kN.m
    MZ  =   165933.6 kN.m

2.4 计算结果对比
2.4.1 简支梁内力分析结果比较
   模型                跨中弯矩（kN.m） 支座反力（kN）
   BEAM4                   164.91                    105.30
   SOLID45                165.85                   105.33
   SOLID65+LINK8     165.933                 105.328
   由上述分析可以看出，运用以上三种不同的单元类型对简支梁进行有限元建模，计算结果和力学方法计算结果的吻合情况较好。（力学方法计算出梁跨中弯矩为165.85kN.m，支座反力为105.3kN）

2.4.2 模态分析结果比较
分别运用ANSYS与SAP2000对所建模型进行模态分析。其中，ANSYS运用BEAM4单元与SOLID单元建立的模型为空间梁模型，其振型除了有平面内的振动外，还有平面外的振动，其自振频率见表所示：
         阶数             BEAM4（平面）                 SOLID45                SOLID65+LINK8
           1               9.5522                        11.92                       9.7
           2               38.135                        20.306                     17.1
           3               47.484                        40.506                     32.3
           4               85.528                        69.11                       53.3
           5               129.52                        69.498                     59.0
   ANSYS运用BEAM3单元与SAP2000建立的为平面简支梁模型，同时使用实体模型建立简支梁约束条件，使模型为平面内振动。两种计算方法的频率见表所示：
         阶数          BEAM3                       SOLID65+LINK8                  SOLID45            SAP2000
          1             20.963                         17.649                       24.958            20.833
          2             83.079                         55.133                       80.081            80.662
          3             132.81                         87.389                      117.33             132.26
          4             184.13                         152.47                       192.37             168.7
          5             320.76                          224.65                      299.07             256.98
   由上述两表可以看出，对于空间梁单元模型，运用ANSYS中BEAM4单元模拟，虽然将其约束定义为平面梁单元，但是其自振形式为空间振动，由于单元差异，导致结构自振频率相差较大。
相对于空间梁模型，平面简支梁模型在两种软件中的自振频率相差不大，只有第五阶频率有差异，且其振动形式相同。

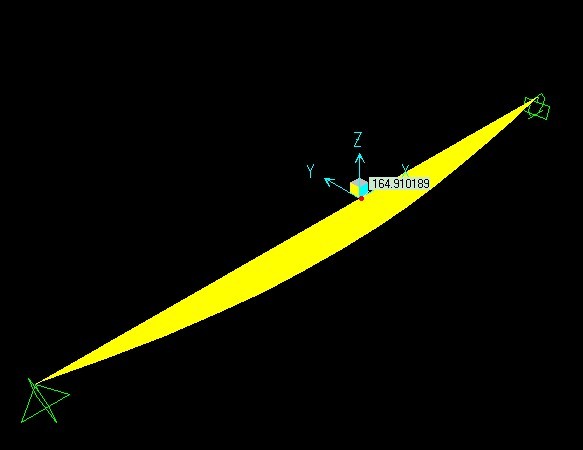
3 利用SAP2000建立模型与求解
    下图为利用SAP2000软件建立简支梁模型，对其进行静力计算所得跨中弯矩，为164.9kN.m，与ANSYS软件的计算结果基本吻合。

4   节点分析
    模型建立：取梁1/4跨度到中间跨度的梁段作为分析对象，如下图所示：

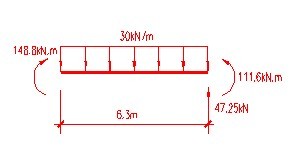
    此简支梁1/4模型在不考虑重力的情况下可靠自身节点受力达到自身平衡。其中梁上表面受竖直向下均布力120kN/m2，右端截面受剪力47.25kN，弯矩111.62815kN.m，左端截面受弯矩148.8375kN.m，此节点在上述荷载作用下可自平衡，受力图如下图所示：

5 结论
   （1）本文通过ANSYS有限元软件中3种不同单元建立了简支梁模型，经过同种工况计算，结果基本相同。
   （2）将ANSYS计算结果与SAP2000以及力法计算结果进行了对比，验证了计算结果的正确性。
   （3）对简支梁有限元模型进行了模态分析，得出了不同单元下简支梁的自振频率。
   （4）提取跨中1/4长度简支梁，对其进行了自平衡计算，对1/4构件施加提取内力，该构件能够在内力作用下自平衡。